[(Programmers 강의) Algorithm with Data Structure 03강. 정렬과 탐색(Sorting & Searching)]
정렬과 탐색(Sorting & Searching)
00. 들어가기에 앞서
-
람다함수(lambda)
-
런타임에서 생성, 사용할 수 있는 익명 함수
-
주로 filter(), map(), reduce()와 같은 전형적인 기능 개념과 함께 사용
-
쓰고 버리는 일시적인 함수
-
함수가 생성된 곳에서만 필요
-
간단한 기능을 필요한 곳에서 즉시 사용하고 버림
-
-
-
람다의 정의
lambda [인자리스트]: [표현식]
- return문 포함하지 않음
- 반환값은 표현식에 의해 만들어짐
# 활용 예시
def inc(n):
return lambda x: x + n
f = inc(2)
g = inc(4)
print(f(12))
# 14 (2 + 12)
print(g(12))
# 16 (4 + 12)
print(inc(2)(12))
# 14 (2 + 12)
14 16 14
기능 함수와 같이 쓰는 Lambda
-
- map() : 내장 함수
-
2개의 인자
-
function을 iterable의 모든 요소에 대해 적용
-
function에 의해 변경된 iterator 반환
map(function, iterable)
a = [1, 2, 3, 4]
b = [13, 16, 17, 14]
list(map(lambda x, y: x + y, a, b))
[14, 18, 20, 18]
-
- filter() : 내장 함수
-
2개의 인자
-
interable의 각각의 요소에 대해 Boolean 값 반환
-
True면 남고, False면 제거
filter(function, iterable)
a = [2, 18, 9, 22, 17, 24, 8, 12, 27]
list(filter(lambda x: x % 3 == 0, a))
[18, 9, 24, 12, 27]
-
- reduce() : 외장 함수
-
2개의 필수 인자와 하나의 옵션 인자
-
function을 사용해서 iterable을 하나의 값으로 줄인다는 개념
-
Initializer : 첫 번째 인자로 추가됨
functools.reduce(function, iterable[, initializer])
from functools import reduce
reduce(lambda x, y: x + y, [1, 2, 3, 4, 5], 1)
16
01. 정렬(Sort)
-
정렬이란?
- 복수의 원소로 주어진 데이터를 정해진 기준에 따라 새로 늘어놓는 작업
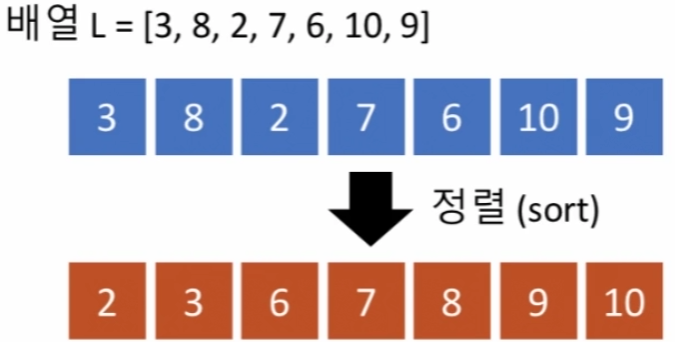
L = [3, 8, 2, 7, 6, 10, 9]
-
Python 리스트의 정렬 1. sorted()
-
내장 함수(built-in function)
-
정렬된 새로운 리스트를 얻어냄
sorted(function) -
sorted(L) # 오름차순
[2, 3, 6, 7, 8, 9, 10]
sorted(L, reverse = True) # 내림차순(Reverse : 역순 정렬)
[10, 9, 8, 7, 6, 3, 2]
-
Python 리스트의 정렬 2. sort()
-
리스트이 메서드(method)
-
해당 리스트를 정렬
list.sort() -
L.sort() # 오름차순
L
[2, 3, 6, 7, 8, 9, 10]
L.sort(reverse = True) # 내림차순(Reverse : 역순 정렬)
L
[10, 9, 8, 7, 6, 3, 2]
-
문자열로 이루어진 리스트의 경우
-
정렬 순서 : 사전 순서(알파벳 순)
-
대문자를 소문자보다 우선
-
문자열의 길이 = 크기 X
- 문자열 길이 순서로 정렬하는 법 : 정렬에 이용하는 키(key) 지정(길이를 키로 지정)
-
L = ['abcd', 'xyz', 'spam']
# 문자열의 길이 순으로 정렬
sorted(L, key = lambda x: len(x)) # lambda 를 사용, 정렬의 키를 지정
# 같은 길이라면 원래의 순서를 적용
['xyz', 'abcd', 'spam']
- 정렬에서 키를 지정하는 또 다른 예
L = [{'name' : 'John', 'score' : 83},
{'name' : 'Paul', 'score' : 92}]
L.sort(key = lambda x: x['name']) # 레코드들을 이름의 알파벳 순서대로 정렬
L
# 레코드? : 여러 데이터의 복합으로 이루어진 데이터 원소
[{'name': 'John', 'score': 83}, {'name': 'Paul', 'score': 92}]
L.sort(key = lambda x: x['score'], reverse = True) # 레코드들을 점수 높은 순서대로 정렬
L
[{'name': 'Paul', 'score': 92}, {'name': 'John', 'score': 83}]
02. 탐색(Search)
- 탐색이란?
- 복수의 원소로 이루어진 데이터에서 특정 원소를 찾아내는 작업.
-
선형 탐색 순차 탐색 (Linear Search Sequential Search) -
리스트의 길이에 비례하는 시간 소요 : O(n)
-
최악의 경우 : 모든 원소를 모두 비교

-
# 선형 탐색 코드 구현
def linear_search(L, x): # L : 탐색의 대상 리스트, x 찾으려고 하는 원소
i = 0
while i < len(L) and L[i] != x: # L의 마지막 원소까지 검사하거나, 찾으면 멈춤
i += 1
if i < len(L): # 리스트 내에 있으면
return i # 찾은 위치 반환
else: # 없으면
return -1
S = [3, 8, 2, 7, 6, 10, 9]
linear_search(S, 6)
4
linear_search(S, 1)
-1
S.index(6) # index() 함수 : 선형탐색
4
S.index(1) # 리스트에 없는 요소를 탐색하면 ValueError
-
이진 탐색(Binary Search)
-
탐색하려는 리스트가 이미 정렬되어 있는 경우에만 적용 가능
-
크기 순으로 정렬되어 있다는 성질 이용!
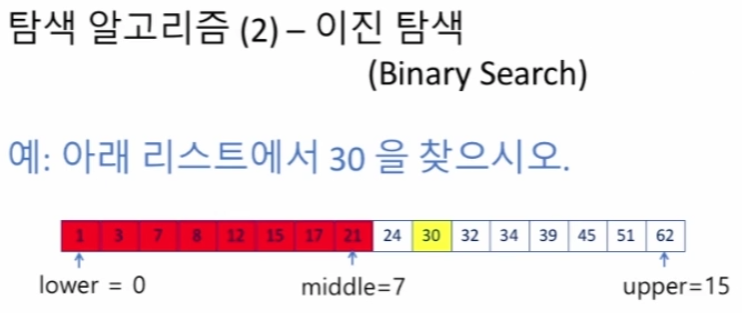
-
lower, uppper, middle 생성 후, middle과 탐색값 비교
-
탐색값 == middle : 탐색 완료
-
탐색값 > middle : lower ~ middle 무시
-
탐색값 < middle : middle ~ upper 무시
-



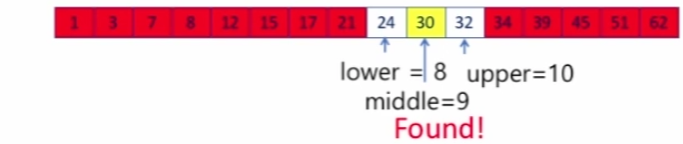
-
한 번 비교가 일어날 떄마다 리스트 반씩 줄임(Divide & Conquer) : O(log n)
- 분할정복(Divide & Conquer) : 기존의 문제를 해결하기 쉬운 단위로 나눠서 해결한 후 다시 합침
-
# 이진 탐색 코드 구현
def binary_search(L, x):
lower = 0
upper = len(L) - 1
idx = -1
while lower <= upper:
middle = (lower + upper) // 2
if L[middle] == x:
return middle
break
elif L[middle] < x:
lower = middle + 1
else:
upper = middle - 1
return -1
S = [1, 3, 7, 8, 12, 15, 17, 21, 24 ,30, 32, 34, 39, 45, 51, 62]
binary_search(S, 30)
9
binary_search(S, 31)
-1
-
선형 탐색과 이진 탐색의 성능 차이
-
10만개의 원소 중, 1000개의 숫자를 찾아보기
-
결과(강사님의 예시)

-
효율적인 자료구조, 알고리즘을 사용해야하는 이유 : 성능 차이
-
무조건 이진 탐색이 옳은게 아니라, 때에 따라서는 선형 탐색이 더 나을 수 있음
-
03. 과제
3강 실습(Link)
def solution(L, x):
lower = 0
upper = len(L) - 1
while lower <= upper:
mid = (lower + upper) // 2
if L[mid] == x:
return mid
break
elif L[mid] < x:
lower = mid + 1
else:
upper = mid - 1
return - 1

댓글남기기