[(Programmers 강의) Algorithm with Data Structure 04강 ~ 05강. 재귀 알고리즘(Recursive Algorithms)]

재귀 알고리즘(Recursive Algorithms)

01. 재귀함수

• 재귀함수(Recursive Algorithm)란?

  • 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 것

  • 생각보다 많은 종류의 문제가 재귀적으로(recursively) 해결 가능

  • CS(Computer Science) 분야에서 자주 사용

  

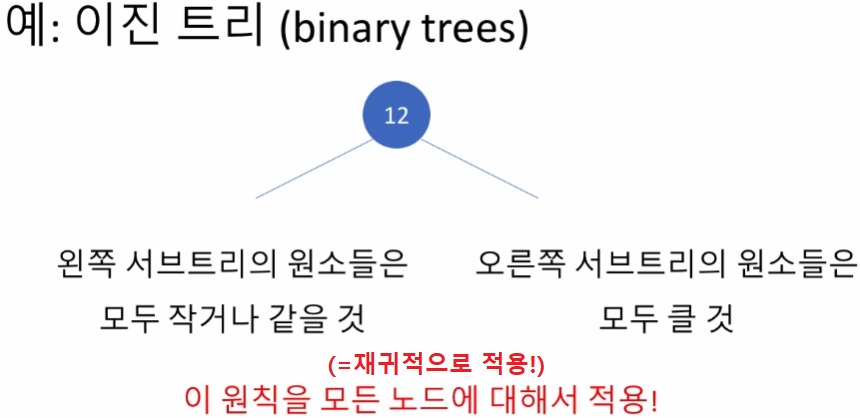
    - 이진 탐색과 비슷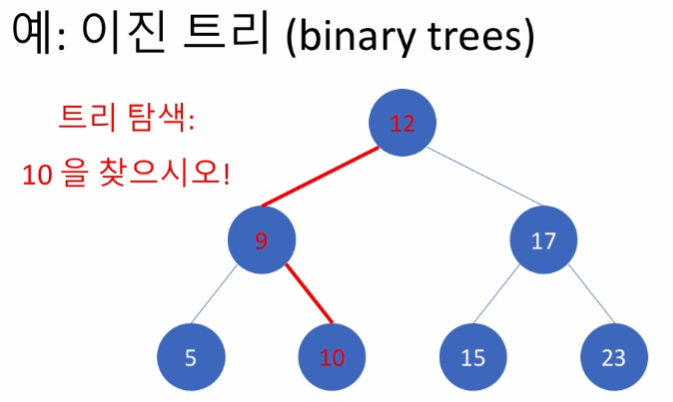
  

  

    - 이진 트리는 이진 탐색과 비슷한 흐름을 재귀적인 트리 알고리즘으로 구성
  

  

  

    - 함수 내에서 자기 자신을 호출
  

# 자연수의 합 재귀 알고리즘(RecursionError)

def sum_num(n):
    return n + sum_num(n - 1)

sum_num(10)

# Maximum recursion depth exceeded
# RecursionError
# 음수영역까지 끝없이 재귀하기 때문

def sum_num(n):
    print(n)    # 어떻게 실행되고 있는지 확인하기 위한 코드(디버깅)
    return n + sum_num(n - 1)

sum_num(10)

10
9
8
7
6
5
4
3
2
1
0
-1
-2
-3
-4
(중략)
-2950
-2951
-2952
-2953
-2954

# 자연수의 합 재귀 알고리즘

def sum_num(n):
    print(n)
    if n <= 1:
        return n
    else:
        return n + sum_num(n - 1)
    
sum_num(4)

4
3
2
1

10

• 재귀 호출의 종결 조건(trival case)

  • 위 예제에서 확인했다 싶이 재귀 호출은 종결 조건(trival case)이 매우 중요

  • 일반적 구조

  
    def function(x):
  
        if n ...:
  
            ...
  
            # 매우 중요!
  
        else:
  
            ...
  
            function(...)
  
  

• 재귀 알고리즘의 효율

  • 모든 재귀 알고리즘은 대칭되는(Counter-Part) 반복 알고리즘이 존재

  

    - 시간복잡도 자체는 같으나 효율을 비교하면 다른 문제
  
    - 위 예시의 효율성
  
    - Reculsive Ver은 함수를 추가로 호출하는 부수적 동작 존재
  
    - 따라서 Iterartive Ver보다 효율성이 떨어진다고 볼 수 있음
  
    - 사람이 생각하는 방식을 표현하기에 유리하나
  
    - 효율적인 측면에서 떨어질 수 있음(**조심해야할 부분**)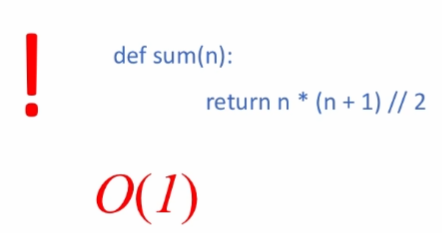
  

  

    - 극단적인 예 : 상수시간의 알고리즘
  

  • 생각보다 많은 문제가 재귀적으로 풀리긴 하지만

  • 또, 재귀적으로 표현된 알고리즘이 사람이 이해하긴 좋지만

  • 컴퓨터가 알고리즘 실행 시, 성능이 반드시 좋지는 않음

  • 효율적인 측면에도 유념해야하기 때문에 알고리즘, 자료구조 선택이 중요

# 추가 예제(! - 팩토리얼)

def fac(n):
    print(n)
    if n <= 1:    # trival case
        return 1
    else:
        return n * fac(n - 1)
    
fac(5)

5
4
3
2
1

120

02. 과제 : Fibonacci 순열

• Interative Ver VS Recursive Ver

  • 둘 다 작성해볼것.

4강 연습문제(Link)

# Interative Ver

def solution(x):
    l = [0, 1]
    if x >= 2:
        for i in range(2, x + 1):
            l.append(l[i - 1] + l[i - 2])
    return l[x]

solution(8)

21

# Recursive Ver

def solution(x):
    if x == 0:
        return 0
    elif x <= 2 :
        return 1
    else:
        return solution(x - 1) + solution(x - 2)

solution(8)

21

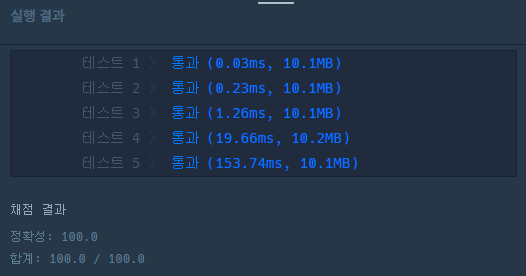
• 확실히 Interactive Version이 더 빠른 실행 결과로 통과했다.

# Recursive Ver
# 강사님 코드
def fibo(n):
    if n <= 1:
        return n
    return fibo(n - 1) + fibo(n - 2)

fibo(8)

21

03. 재귀함수의 유용성

• 재귀 알고리즘을 통해 다음 문제 해결

  • 조합의 수(n 개의 서로 다른 원소에서 m개를 택하는 경우의 수) 구하기

    • 재귀적이지 않은 방법으로 해결

  

    - 재귀적으로 방법으로 해결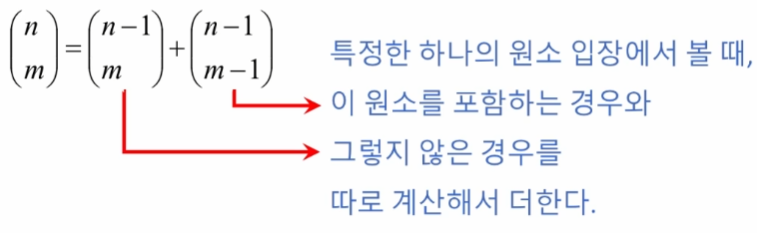
  

  

    - 잘못된 방법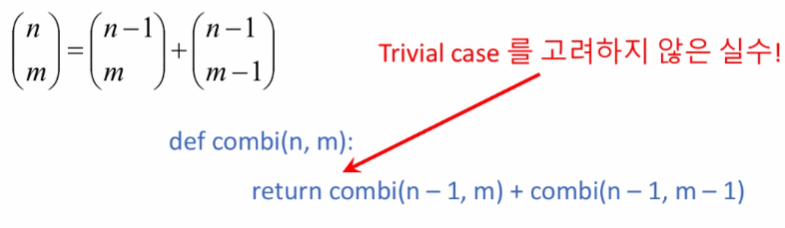
  

  

    - 올바른 방법
  

  

    - 하지만 효율성 측면에서는 여전히 좋지 않다
  
    - combi를 계속해서 호출하기 때문
  
    - 그렇다면 왜 재귀함수를 쓸까?
  

• 하노이의 탑 문제

  • 재귀 알고리즘이 효율은 떨어진다고 하더라도 사람이 생각하는 방식을 코드로 직접 옮김으로써 유용한 경우가 있다.

  • 그 대표적 예가 이 문제

  • 한 기둥의 원반들을 전부 다 다른 원반으로 옮기는 문제.

    • 단, 더 큰 원반은 더 작은 원반의 위로 올라갈 수 없음

  • 이 문제를 재귀적 알고리즘을 통해 해결하면 편함.

    • 나중에 한 번 해볼것!

# 하노이의 탑 도전(작성 예정)

• 아주 많은 자료구조에 있는 문제 中 트리에 해당하는 문제는 재귀 알고리즘으로 푸는게 적당할 수 있음

  • 연습문제(빈칸채우기) : 재귀적 이진 탐색

  

04. 과제 2

5강 연습문제(Link)

def solution(L, x, l, u):
    if x < L[l] or x > L[u]:
        return -1
    mid = (l + u) // 2
    if x == L[mid]:
        return mid
    elif x < L[mid]:
        return solution(L, x, l, mid - 1)
    else:
        return solution(L, x, mid + 1, u)